Net Present Value
Net Present Value measures the difference between present value of future cash inflows generated by a project and cash outflows during a specific period of time. With a help of net present value, we can figure out an investment that is expected to generate positive cash flows.
In order to calculate the net present value (NPV), we first estimate the expected future cash flows from a project under consideration. The next step is to calculate the present value of these cash flows by applying the discounted cash flow (DCF) valuation rules. Once we have the estimated figures then we will estimate NPV as the difference between present value of cash inflows and the cost of investment.
NPV Formula:
NPV=Present Value of Future Cash Inflows – Cash Outflows (Investment Cost)
In addition to this formula, there are various tools available to calculate the net present value e.g. by using tables and spreadsheets such as Microsoft Excel.
Decision Rule:
An investment should be accepted if its Net Present Value is positive and rejected if it is negative.
The NPV has an expression. I have been trying to stay away from expressions and equations as much as we could. Remember and it is important that you keep in mind once again, that because our time in this course is very limited, it is important that you keep in mind that each of these. Sessions comes with a rating that you can do either before or after. Typically, it’s better to do it after. In order to actually extend many of the formal content, the expulsions, and the equations, we have not actually covered here. But they’re covered in the readings. Therefore, it is important that you remember that after each session, there is going to be a reading. And only after you do that rating you can go and work on the on the problem said that will ask you to apply some of the concepts that we’ve been discussing here.
Now this is one exception, I do want to put there the expression for the NPV. And not only because it is very important, but also because we need to run a calculation. And that calculation we can’t really run unless we have the expression right in front of us, as you’re having there on your screen. So on the left-hand side, we simply have the definition. That we are going to calculate an NPV, that is, a net present value. On the right-hand side, we could have written what you see there in more than one way. And by more than one way, I mostly think that, that you know. We could have maybe used different notation. The expression is more or less given. So let us make a few comments to make sure that you understand what that expression means. Let’s go to the first cash flow on the wrong, right-hand side. That is CF0. That is basically a, the first cash flow that because it happens today, that’s what the 0 means, that it’s going to happen today. You are not going to be discounting.
Remember what we discount are things that are going to happen in the future, and we discount those things because a dollar that you receive one, two or three years from now does not have the same value as a dollar you receive today. So basically we can to apply that discounting. In the complementary reading that comes with this session, there is a little bit of more discussion and a couple of examples that will help you understand this whole idea of present value. But for now and for our purposes it’s a very basic idea that you know, if I offer you what do you prefer a dollar today, or a dollar a year from today? Or a dollar today, or a dollar two years from today, the sooner you get that dollar the better. Because the more you wait to get that dollar, the more than that dollar will lose value to inflation. And that’s what we called before, losing purchasing power. So we need to discount because of that reason. The further away that dollar comes. The higher the discount rate we need to apply.
Now, that first cash flow, not being discounted, means that this is an amount of money that is related to today. And I’m saying that it is related rather than it is positive or negative simply because it doesn’t have to be a negative cash flow. Most people actually write a negative sign next to that C of 0, and that basically means, well that’s some sort of initial investment that we need in order to start this particular project. And that’s typically the case, but it doesn’t have to be the case. You know, sometimes and you can think a typical example may be executive education programs that are running business schools. In those programs actually sometimes, you first get the cash flows when people sign up for the program. And then you have to deliver and therefore bear the cost. So it is not entirely clear and it doesn’t have to be the case that the first cash flow is negative, but more often than not, it is true that it is. So if it makes you feel better and you want to put a negative sign on top, in front of that cash flow. And that is just fine, but for now just think of that as some sort of initial investment that we need in order to get the project started. Now, the other cash flows as you see, all of them are discounted, and that DR is the discount rate. We are going to get back to the discount rate later on.
For now, we could think of it as the cost of capital the company’s cost of capital and that is exactly what we have done before that is in sessions three and four. We thought about and we calculated the cost of capital for Starbucks if you remember, and we are going to go back to Starbucks a little bit later on. Those cash flows as you see are being discounted by a discount rate, but also notice that as we move from the left to the right that there is something that increase and that is the power at which we raise 1 plus DR. Well, what that means is that that discount factor is getting bigger and bigger and bigger, and that is just a little technical way of saying what we said before, that the further away the cash flow is in the future. The higher the discount rate we are going to apply. Second thing that is important about all the other cash flows that are being discounted.
Remember, if the discount rate is the cost of capital, but if it is not, it could be any discount rate. That discount rate is always going to be positively related to risk and that is an important thing to keep in mind, because it tells you that everything else equal the riskier the project that we evaluate, the higher that discount rate is going to be. So everything else equal, if we were comparing two projects which deliver the same cash flows, but one is riskier than the other, then the discount rates we’re going to be applying to the riskier ones are going to be higher. And as you see in that expression, the net present value is going to be lower. Third and final thing. And this is probably the most important things about those about those cash flows. And that is, all those are expected cash flows. We wish that we knew those cash flows with certainty. But in real life, we never know. You know, we make investments, we have an expectation of what we’re going to get out of those investments, but any corporation, you know, any corporation at any given point in time can only expect, can never actually foresee exactly what those cash flows are going to be. And here’s, you know, something for you to keep in mind.
When you are evaluating a project, the throwing numbers into an NPV expression, that is the very easy part. You know, if I tell you, let us evaluate this project, as we will do a few minutes from now. And I’ll give the expected cash flows and I’ll give you the discount rate, then throw in those numbers into excel and coming up with a net present value that is not very difficult. The difficult part in real life, obviously, is to forecast, to foresee what those cash flows are going to be. So, I, I didn’t put an expected sign, when, you know, technically speaking, I should have put an expectation before each of those cash flows from one to t but I didn’t want to over-complicate, unnecessarily the expression. But remember that anything that comes in the future cash flows one to all the way to t where t is any number, it could be five years, ten years, 15 years, whatever you think is the length of this project, whatever you think is the number of periods from where you can foresee. What the cash flows are going to be.
During all these periods, these cash flows are simply going to be expected. And of course, the real key to evaluating a project, that the more accurate you are in forecasting those cash flows, the better investment decisions you’re going to make. And here, you know, in finance we can’t help you a whole lot. Knowing a company, knowing the sector, knowing how the economy’s going to evolve might actually give you an edge. In forecasting cash flows compared to a financial expert, that does not know this company, this industry or how the economy is going to, to perform. All right? So that’s it for the expected cash flows.
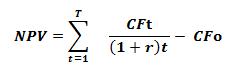
Thank u, Its been a real help to me that i found such a good answer
You made a few excellent points there. I did a search about the topic and barely got any specific details on other sites, but then great to be here, seriously, thanks.
– Lucas